Google Summer of Code 2025 midterm blog post
Introduction
Welcome to the midterm update on my progress with the WeatherRoutingTool tool as part of Google Summer of Code 2025.
In the initial phase of GSoC 2025, my primary focus has been on refining and enhancing the genetic algorithm utilized in the WeatherRoutingTool (WRT) for ship route optimization. My methodology began with a precise definition of the optimization challenge, followed by a thorough comprehension of the algorithm’s existing implementation. I also established a performance baseline to facilitate quantitative assessment of subsequent improvements.
Problem Definition
To enhance the Genetic Algorithm (GA) for ship route optimization, my initial efforts have concentrated on two key areas: clearly defining the optimization problem by establishing its scope, and setting up a method to measure baseline performance. This approach will allow for a quantifiable assessment of the algorithm’s improvements.
The WeatherRoutingTool’s genetic algorithm approaches the pathfinding challenge as a waypoint optimization, employing a permutation-based discrete genetic algorithm. The population is created using a grid-based method, which facilitates the establishment of a performance baseline through deterministic search methods and offers a controlled experimental setting.
Permutation-based Discrete GA Design Rules
The implementation of the genetic algorithm is guided by the following design rules.
- Search space is discrete and combinatorial
The search space consists of all possible permutations of the original set of waypoints. No new waypoints are added or removed. The final path is always sampled from the initial set of waypoints - Diversity of initial population
Excessive or uncontrolled diversity leads to low-quality, infeasible and poor-performing routes, which slows convergence. - Order-dependent fitness
Changes in waypoint order can lead to large changes in the fitness function. Thus, choice of crossover and mutation need to enforce order maintenance. - Need for controlled mutation
Permutation-based problems quickly converge to a local optimum.
GA Constraints
These design rules lead to the following implementation constraints.
- Population requires valid permutations
Each chromosome must represent a valid path, visiting each exactly once. Overlapping and repeated waypoints are not allowed. - Crossover implies ordered shuffling of waypoints between the two parents
During Crossover, waypoints from both parents must be combined while preserving the population constraints (no repeat, all required points included). Standard crossovers for binary or real-valued points don’t work here. - Mutation
Mutation of permutation-based chromosomes implies a slight random change in the order of the waypoints, either by swapping two waypoints, or shuffling a small segment by sampling the routes from the other reachable waypoints.
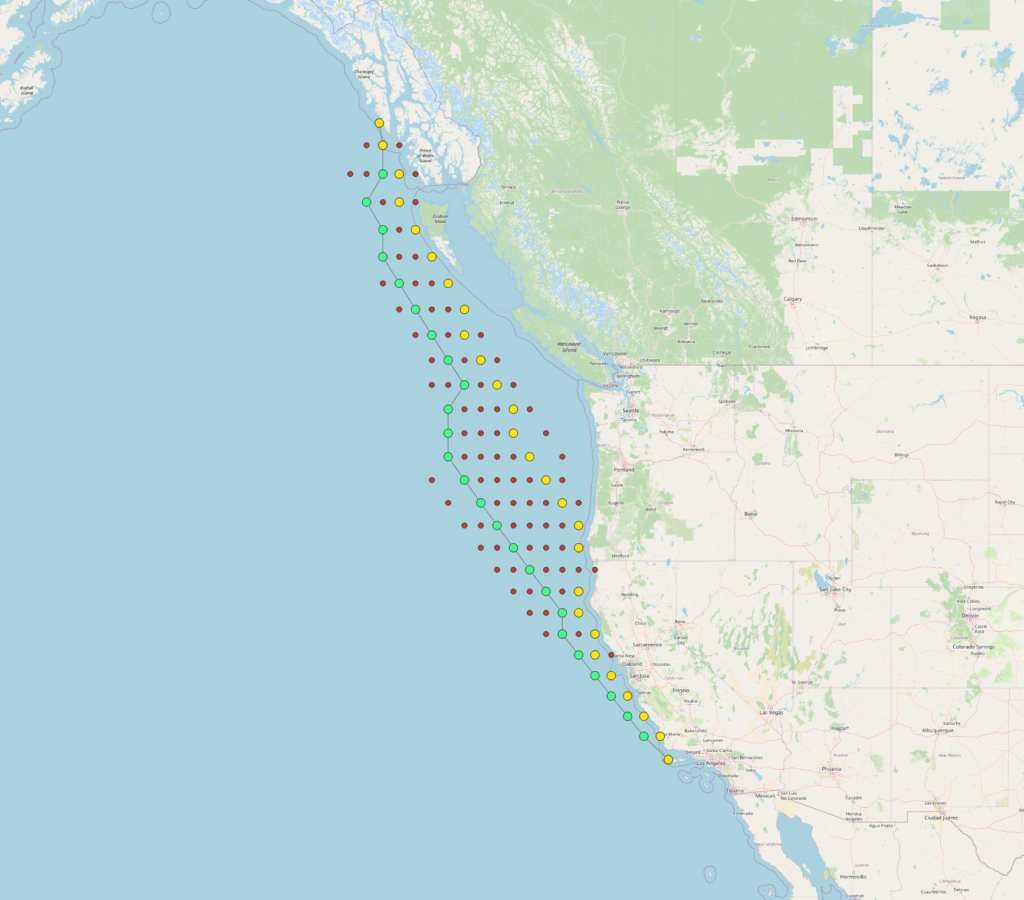
red: initial population
green: deterministically best path with least fuel consumption
yellow: genetic algorithms performance
Performance Evaluation
To evaluate the Genetic Algorithm (GA), I have considered the following two approaches.
- Establishing a Baseline with Deterministic Search: A grid-search deterministic approach (A* search) is employed to identify a fuel-optimal path through a set of waypoints. This establishes a baseline performance against which the GA’s performance can be measured.
- Monitoring GA Convergence: The convergence of the fitness function over generations is documented to track performance improvements within the GA itself.
This deterministic baseline serves a dual purpose.
- Validation of GA Optimality: If the GA’s performance aligns with the deterministic approach, it suggests that the GA is capable of reliably finding optimal or near-optimal permutations of the route.
- Discovery of Novel Solutions: If the GA surpasses the performance of the deterministic approach, it indicates the GA’s ability to discover new waypoints, leading to long-term route optimization.
Improvements
To improve Crossover and Mutations while adhering to the suggested algorithm design rules and constraints, I propose the following approaches.
Crossovers
Modeling my algorithm genomes as a permutation-based waypoint route implies the need for maintaining order and a no-repeat criteria on the individuals produced after crossover. So I am considering a PMX crossover operation
PMX Crossover
Partially Mapped Crossover utilizes two crossover points to split each parent into 3 segments. The middle segment of each parent is inherited directly by the corresponding child and the far end segments are filled using a mapping relationship derived from the swapped segments. This ensures the no-repeat/duplicates and ordering criteria.
Steps
- Choose two crossover points (defining a middle segment).
- Copy the middle segment from each parent into the child at the same position.
- Build mappings for swapped elements to resolve conflicts in the remaining positions.
- Fill in the rest of the child using the mapping to ensure all waypoints are included exactly once.
Mutations
The following mutation operators are being considered, each carefully designed to maintain valid permutations.
Examples of possible mutation operators
- Swap mutation
Pick two positions at random and swap their waypoints - Inversion
Pick a random segment in an individual and reverse the segment - Scramble
Pick a random segment in an individual and randomly shuffle the segment - Insertion mutation
Remove a waypoint from its current position and insert it at another position
Upcoming work
For the upcoming part of the GSoC timeline, I aim to achieve continuous route path optimisation using the following approach for waypoint injection and route smoothening
Continuous Route Optimization
Grid-based initial population results in non-smooth routes more concerned with waypoint optimization over route optimization. In order to produce continuous and smooth routes, there are two main approaches.
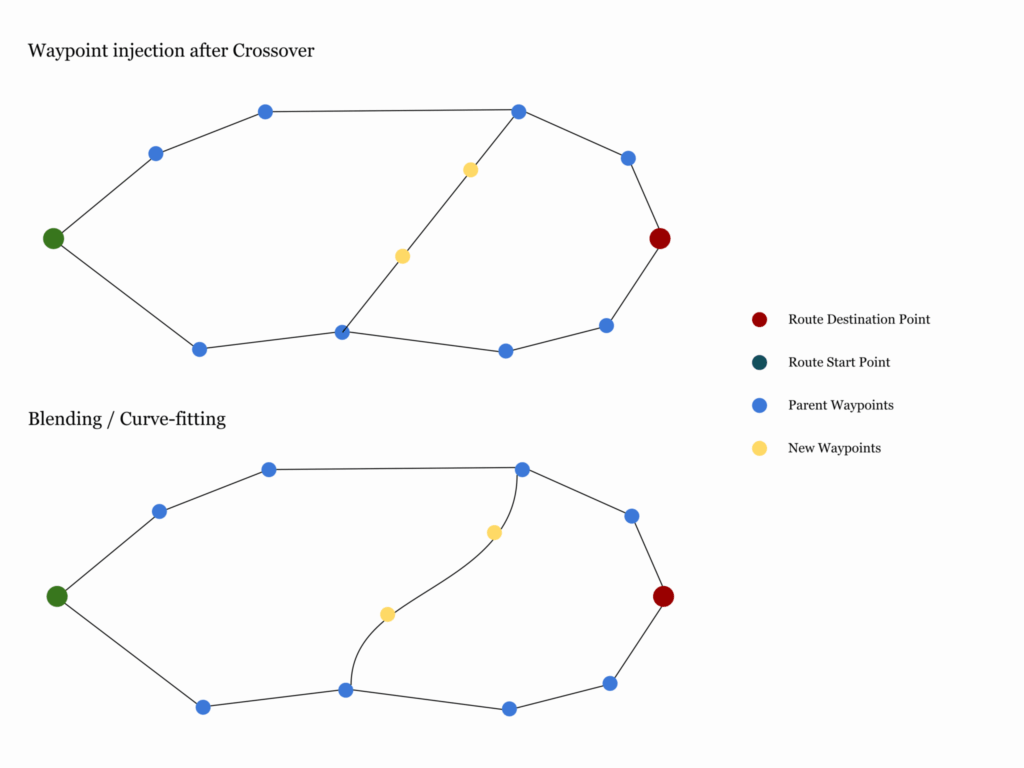
- Waypoint Injection after Crossover
When crossing over diverse routes, we introduce new waypoints between crossover points to help smoothen our fitness estimation. This leads to new waypoints in the search space. - Blending and/or Curve-fitting
Blending generates offspring by taking a weighted average of the corresponding genes from two parent chromosomes. This approach helps smoothen our route further, producing more continuous routes over iterations.
Conclusion
The initial phase of my GSoC 2025 project has focused on precisely defining the scope and limitations for the algorithm’s implementation. This involved a detailed analysis of potential constraints and functionalities, establishing a strong foundation for development. Simultaneously, I’ve been researching and evaluating various methods to assess the algorithm’s performance and accuracy. This comprehensive evaluation approach will be vital for validating the WeatherRoutingTool’s effectiveness and identifying areas for improvement.
References
- https://www.baeldung.com/cs/ga-pmx-operator
- Continuous Development Issue: https://github.com/52North/WeatherRoutingTool/issues/44
- Practical Genetic Algorithms by Randy L. Haupt and Sue Ellen Haupt
These developments took place in connection with the TwinShip project.
 This work has been co-funded by the European Union’s Horizon Europe programme under grant agreement No. 101192583
This work has been co-funded by the European Union’s Horizon Europe programme under grant agreement No. 101192583
Leave a Reply